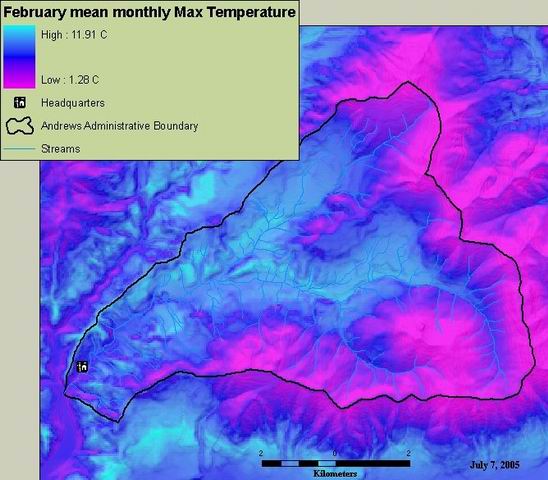
Original datasets consisted of daily mean, maximum and minimum temperatures that had been quality-checked and processed into a consistent format. Missing data were indicated and questionable values were flagged according to a number of conditions (Bierlmaier, pers. comm.) Any value flagged in any way during this first filtering process was immediately discarded from the database and transformed into a missing value for that day. Daily temperatures were graphed and visually analyzed again on monthly and yearly scales to check for erroneous values possibly missed during the first filtering process. Again, any questionable values were discarded, ensuring the most reliable possible dataset. For the MET sites with variable sensor heights, the 1.5 meter values were used unless that value was missing, in which case the next lower sensor (2.5 meters) was used. After filtering twice, any site left with less than three years of data (10% of the 30-year period) was discarded. The GR sites were an exception to this rule because of their strategic locations in underrepresented areas or next to open MET sites (making them ideal for open/closed canopy comparisons). Most discarded sites are in areas that are adequately represented spatially by long-term sites. After mean monthly maximum and minimum temperature datasets were adjusted with regression functions to simulate open flat sites, they were imported into PRISM. PRISM uses a combination of geographic and statistical methods to spatially interpolate climate variables (Daly et al., 1994). It is a coordinated set of rules, decisions, and calculations (an ‘inference engine’) designed to mirror the decision-making process an expert climatologist would use in making a map (Daly and Johnson, 1999). Weights are assigned to the point data according to various factors. A station is downweighted when its elevation differs significantly from that of the target cell or is far from it geographically. The station’s influence is further reduced if it is clustered with others (avoiding over-representation), or has a significantly different slope and aspect (topographic facet) than the target cell (Daly et al., 1997). When used on large areas, PRISM is able to consider a station’s proximity to the ocean and the ‘flatness’ of an area to determine whether two-dimensional or three-dimensional estimates should be used (Daly and Johnson, 1999). These last two factors are not important in this study, because the HJA is a small area 150 kilometers from the nearest ocean and is hilly enough to require only the three-dimensional model. An iterative approach was taken in creating the gridded data for the temperature maps. With the exception of the stream sites, all canopy/topography-adjusted maximum and minimum temperature datasets were initially input into PRISM, using default parameters and a single-layer atmosphere model. The resulting grids clearly showed which sites to initially discard. For example, the unusually warm sites RS38, RS89, and H15MET were visually obvious as high temperature ‘bulls eyes’. All GR sites were revealed to be anomalously warm and were also discarded. Other sites such as CS2MET, RS02 and RS86 were also discarded because of warm or cold spatial biases. Including RS01’s data caused unusual temperature patterns due to the seasonal presence of Blue River Reservoir. From initial PRISM modeling and personal experience, VANMET was known to be anomalously warm and RS04 anomalously cool. In order to retain spatial representation in their area, a ‘pseudo-site’ was created at point between them on the DEM, with temperature values given as their averages for each month. Using this pseudo-site instead of VANMET and RS04 individually gave far more realistic temperatures on top of the northern peaks and ridges of the HJA. The National Climatic Data Center’s 500-millibar (approximately 5200 meters) 2.5° global temperature grid was used as a high-level anchor ‘site’ over the HJA to ensure that the tops of the highest peaks and ridges in the area were modeled correctly. Table 4.26 summarizes the sites used in the final analysis. With the exception of the Mack Creek area, most regions within the HJA are fairly well-represented spatially, having a measurement station within about two kilometers. PRISM was run again with the reduced set of sites. Since the number of sites had been decreased to 15, the radius of influence was specified to consider every point in the HJA when making cell estimates. Even using a single atmospheric layer model with this specification, a temperature inversion over the lower Lookout Creek Valley was evident during most months for both maximum and minimum temperatures. The maximum temperature inversion is more defined in January (at an elevation of approximately 700 meters), with minimum temperature inversions well-defined in both January and July at approximately 720 meters. Taking the base elevation of the Lookout Creek valley to be 420 meters, depths of inversions over it were approximately 280 meters for maximum temperatures and 300 meters for minimum temperatures. We thus switched to the two-atmosphere model in PRISM with these inversion height values specified. A certain amount of ‘cross-talk’ was allowed between layers to avoid an unnaturally abrupt transition between layers. Elevations were buffered by ± 150 meters for maximum temperature and ± 120 meters for minimum temperatures, reflecting the higher seasonal variation in minimum temperature inversion heights. Variable inversion heights with elevation were modeled such that the deepest inversions were found at the lowest elevations (over the lower Lookout Creek and McKenzie River valleys). The two-layer atmosphere model was used to model both maximum and minimum temperatures for every month. All of the final parameter values used to make the grids were determined by varying them slightly in different combinations, then iteratively running PRISM and analyzing the results both statistically (with regression functions through the PRISM interface) or visually (with the temperature grids). In this way, knowledge of HJA microclimatology could be applied and combined with PRISM’s statistical abilities to create maps that were not only numerically sound, but made sense physically. Citations for PRISM: Daly, C., E.H. Helmer, and M. Quinones. 2003. Mapping the climate of Puerto Rico, Vieques, and Culebra. International Journal of Climatology, 23: 1359-1381. Daly, C., W. P. Gibson, G.H. Taylor, G. L. Johnson, P. Pasteris. 2002. A knowledge-based approach to the statistical mapping of climate. Climate Research, 22: 99-113. Daly, C., R.P. Neilson, and D.L. Phillips. 1994. A statistical-topographic model for mapping climatological precipitation over mountainous terrain. Journal of Applied Meteorology 33: 140-158.